Counter-Optimization Library (colibry) for MATLAB

The Counter-Optimization LIBraRY (COLIBRY) is a modular MATLAB / Simulink software package featuring a rich collection of optimization and optimal control-based testing methods that can be used to investigate the worst-case behavior of your system. The methods are primarily targeted towards testing dynamic systems regarding worst-case inputs and parameters. Most importantly, COLIBRY’s user interface is designed in such a way that testing routines can be set up in minutes by means of an easy and intuitive syntax.
What is Counter-Optimization?
Counter-optimization refers to a branch of testing methods in which optimization and optimal control strategies are employed to search for violations of design criteria. These methods have so far proven to be exceptionally successful in identifying worst-case solutions. To a large extent, this is contributed to the effectiveness and high computational efficiency of the numerous optimization and optimal control algorithms available today. Moreover, compared to standard testing procedures (e.g. based on parametrized tests using sampling / gridding approaches), these methods can be useful to determine violations in between grid points, which may otherwise be missed.
COLIBRY is an application-centered toolbox that offers analysis methods such as:
Linear Optimal Control-based Analysis

An optimal control-based method that identifies worst-case control inputs to quasi-linear systems. Quasi-linear systems are understood here as linear models subject to additional state constraints. These constraints can be used, for example, to model physical limitations such as actuator position and rate bounds. Moreover, by means of post-optimal sensitivity analysis, the influence of parameters on the worst-case value of the testing criterion can be computed efficiently. For an application of this method a linearization routine, capable of computing the linearized system, input, and output matrix for particular values of the parameters, needs to be provided by the user. The solution obtained from this type of analysis is globally optimal.
Bi-level Linear Optimal Control-based Analysis

By leveraging a two-layered optimization scheme, this method computes the worst-case combination of control inputs and system parameters for quasi-linear systems. On the one side, the lower level in this scheme performs linear optimal control-based analyses for fixed values of the parameters. From a user perspective, the same requirements for the application of this method as for the linear optimal control-based analysis apply. On the other side, the upper level solves a (typically low-dimensional) parameter search problem. Several optimization methods such as gradient-based or global schemes can be chosen by the user for the upper level. Note that despite their efficiency and the ability to check the optimality conditions for local solution candidates, gradient-based methods do not guarantee the identification of globally optimal solutions for the parameter search. Similarly, global methods are to be understood here in the sense that in practical applications these methods can increase the chance of identifying a globally optimal solution. The same holds for the use of global optimization methods in the single shooting-based analysis.
Nonlinear Optimal Control-based Analysis
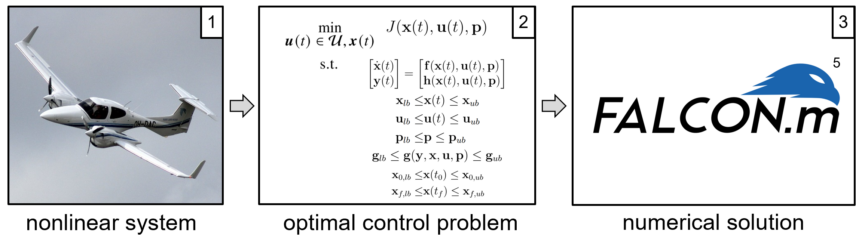
This method implements an interface for the application of direct optimal control methods. In the current version of COLIBRY this interface maps to FALCON.m. Using FALCON.m, the nonlinear optimal control problem is transcribed to a discretized version that can be efficiently solved using sparse Nonlinear Programming (NLP) solvers. Under this approach, the optimization of control inputs and parameters can be treated simultaneously. The FALCON.m framework and its dependencies, such as additional NLP solvers, represent a (free) software dependency outside COLIBRY. For the application of this method, the closed-loop system under test needs to be implemented as a model understood by FALCON.m. In particular, that requires implementing a procedure for the efficient computation of partial derivatives. Despite there being no guarantee of finding a globally optimal solution, the necessary and sufficient conditions of optimality can be checked for local solution candidates.
Single-Shooting-based Analysis
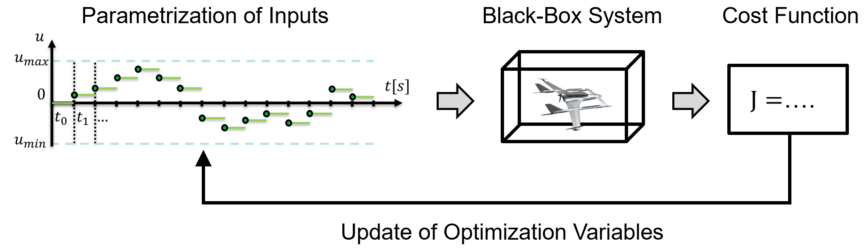
This counter optimization method uses repeated simulation of the SUT to identify detrimental combinations of time-varying control inputs and static parameters. Prerequisite for an application of this method in practice is the implementation of an efficient simulation routine, which then is used within an optimization routine. COLIBRY primarily uses the MATLAB Global Optimization Toolbox to solve the underlying, typically nonlinear, black-box-type optimization problem. Recalling the remark in the section about the Bi-level Linear Optimal Control-based analysis, the use of global optimization schemes does not guarantee globally optimal solutions.
Learning-based Analysis
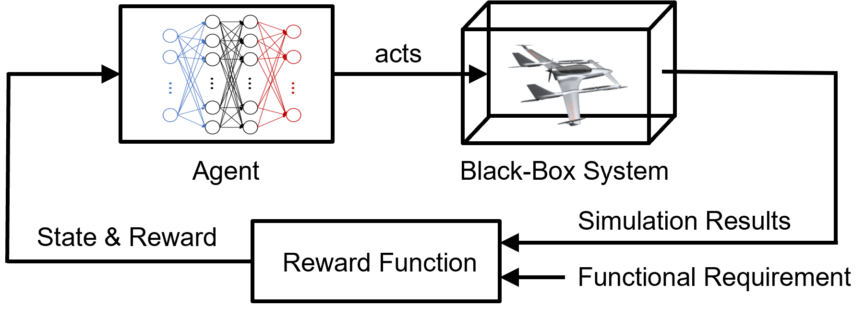
Utilizing RL techniques, this method trains a Double Deep Q-Network agent to identify the worst-case sequence of time-varying system inputs. Because the training of the RL agent constitutes a repeated interaction between the agent and the non-simplified SUT, this counter optimization approach is particularly well suited for the analysis of highly complex systems. However, similar to the single shooting-based approach, this library entry does not provide a guarantee for global optimality.