On this page you can learn more about:
- Radionavigation
- Star Trackers
- Odometry
- Map Matching
- Inertial Sensors
- Aerodynamic Navigation
- Surface-Ranging Navigation
Radionavigation
Radio beacons were the earliest means of aircraft navigation and air traffic control. First radionavigation systems appeared before World War II and presented a network of ground radio stations. In order to get to desired destination pilot was commanded to fly from one beacon to another.
Nowadays a large network of ICAO standardized non-directional radio beacons (NDBs) is widely used in civil aviation. Signal transmitted by NDB is received by onboard automatic direction finder (ADF) that determines direction to the beacon relative to the aircraft and displays it on radio-magnetic indicator (RMI). Air traffic controller can command pilot to follow specific magnetic track either towards or away from the station that is to say to perform QDM/QDR interceptions.
Very high frequency omnidirectional range (VOR) is a further development of short-range radio navigation systems. VOR onboard receiver, unlike ADF, does not need to determine direction to the station, because it is already encoded in transmitted signal. Thus accuracy of radial determination is independent of aircraft’s orientation and wind conditions, which presents a considerable advantage. Distance measurement equipment (DME) is another widely spread means of radio navigation. It is based on request-response technology and allows to measure slant range from airplane to station. There exist more radio navigation systems and technologies. Among them are Loran, Iridium, cellphone positioning, marine radio beacons.
Literature
- W. Monroe and T. L. Bushy, Marine radionavigation and communications. Centreville, Md: Cornell Maritime Press, 1998.
- D. Groves, Principles of GNSS, inertial, and multisensor integrated navigation systems, 2nd ed. Boston, Mass.: Artech House, 2013.
Star Trackers
Stars have been used for navigation since ancient times. For example in the Northern Hemisphere mariners could determine latitude by simply measuring elevation angle of the North Star above the horizon. Celestial longitude determination required in its turn more efforts and additional tools such as nautical almanac and chronometer.
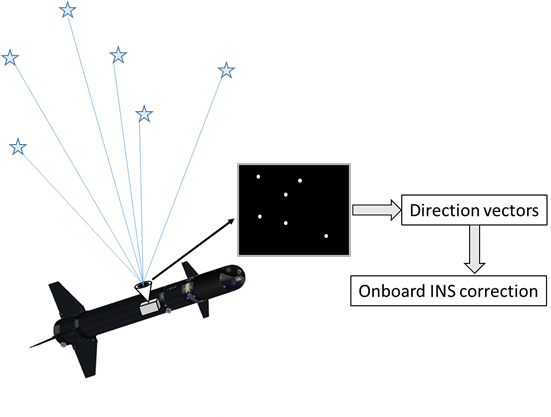
With the advent of inertial navigation stars became a powerful source of globally available aiding information. A star tracker is a device that measures direction vector from vehicle to a star. Early star trackers comprised of a star sensor mounted on gimbaled platform that was commanded to center an image of one star. Direction vector could be calculated from rotary encoder reading. The sensor had a capability to operate both in daylight and at night. Nowadays star trackers are strapdown systems and do not require sophisticated mechanical mounting.
The star sensor is a CCD camera with resolution of about one megapixel whose field of view vary from 8 to 40 degrees. An onboard star catalog includes at least six thousand stars and in case four of them are detected in a unique constellation, they can be identified without any prior knowledge of vehicle’s position and orientation. Application of optimal filtering techniques and accurate measurement models allow to achieve a high quality navigation solution. For more than forty years astro-inertial systems have been used in civil and military applications, such as determination of satellite position, navigation of long range ballistic missiles and airplanes.
Literature
- D. Groves, Principles of GNSS, inertial, and multisensor integrated navigation systems, 2nd ed. Boston, Mass.: Artech House, 2013.
- Kayton and W. R. Fried, Avionics navigation systems, 2nd ed. New York: Wiley, 1997.
Odometry
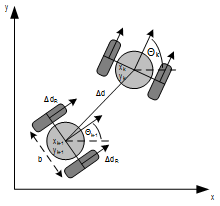
For land based vehicles the distance travelled can be determined from the number of revolutions of the wheels. By using data from at least two opposing wheels also the orientation and course can be deduced. The rotation angle of the drive shaft, typically measured by cog wheels or rotary encoders, is multiplied with the wheel’s diameter to get a distance. More sophisticated models for chassis suspension and tires require specific design knowledge about the vehicle under consideration.
Due to its simplicity, odometry is a very common approach in automotive and robotics applications. Being a kind of dead-reckoning navigation, the errors sum-up with the distance travelled. Typical error sources are:
- Uncertainty of the wheel’s diameter, unroundness, abrasive-wear
- Uncertainty of the wheelbox’ geometry
- Limited encoder resolution and sampling rate
- Irregularities of the ground (cracks, bumps, …)
- Slippage
The first two error sources are deterministic and can thus be estimated and even compensated by appropriate instrumentation and algorithms. Though the latter errors are more of a stochastic nature, their influence can at least be reduced by using redundant sensors.
Because of its error characteristics odometry is mostly used in combination with other navigation aids like GPS or vision systems. Despite its name “visual odometry” does not rely on drive-data but is based on stereo-vision to determine distances and orientations.
Literature:
- A. Adam, E. Rivlin, and H. Rotstein, “Fusion of fixation and odometry for vehicle navigation,” IEEE Trans. Syst, Man, Cybern. A, vol. 29, no. 6, pp. 593–603, 1999.
- J. Borenstein and Liqiang Feng, “Measurement and correction of systematic odometry errors in mobile robots,” IEEE Trans. Robot. Automat, vol. 12, no. 6, pp. 869–880, 1996.
- B. Heißling, M. Ersoy, and S. Gies, Fahrwerkhandbuch: Grundlagen, Fahrdynamik, Komponenten, Systeme: Springer, 2013.
- S. Hesse and G. Schnell, Sensoren für die Prozess- und Fabrikautomation: Funktion – Ausführung – Anwendung ; mit 35 Tabellen, 5th ed. Wiesbaden: Vieweg + Teubner, 2011
Map Matching
Map matching is especially used in land navigation applications, when the platform can in general be assumed to stay on tracks and no off-track operation must be expected. Prominent examples are cars or trucks on streets and trains on railways. Navigation information is matched with a GIS track database to identify the actual track segment and provide an enhanced positioning solution. Map matching conventionally uses navigation information from GNSS together with dead reckoning techniques, like odometry. Dead Reckoning techniques are required to guarantee the continuity of the navigation function.
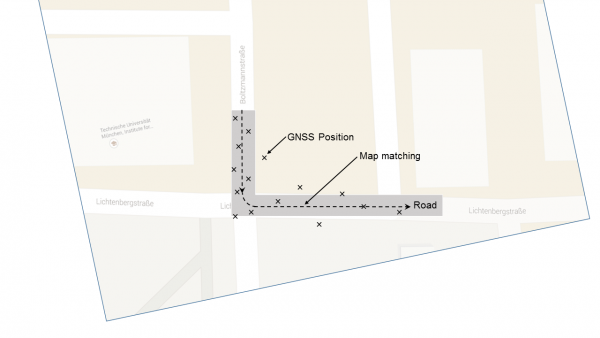
Correct identification of road links is essential for map matching. The simplest method is to select the nearest road link to the positioning solution reported from the onboard navigation system. However, it may become challenging in dense urban areas, since the roads typically get closely spaced, narrower and the positioning performance at the same time poorer due to signal shading and multipath. Advanced methods use a series of reported positions to do the matching using different theories like topological analysis, fuzzy logic, belief theory, etc.
Map matching is strongly dependent upon actual street or railway maps. Hence more and more OEMs provide lifetime map updates and live traffic information for their users. Telematics is key for an Intelligent Transportation System (ITS).
Literature
- Quddus, Mohammed A., Washington Y. Ochieng, and Robert B. Noland. “Current map-matching algorithms for transport applications: State-of-the art and future research directions.” Transportation Research Part C: Emerging Technologies 15, no. 5 (2007): 312-328.
- Groves, Paul D. Principles of GNSS, inertial, and multisensor integrated navigation systems. Artech House, 2013.
Air Data System
Measurements in the local air flow (stagnation point or undisturbed free stream) provide valuable information related to vehicle state.

Air data measurements are performed by either a multi-hole probe or a single-hole probe with vanes. Impact pressure and aerodynamic angles of attack and sideslip govern aircraft aerodynamic forces and moments and can directly be observed.
Barometric height computed from absolute air pressure based on a standard model and adjusted to an agreed level (local or standard QNH) is used as vertical indication for air traffic control and flight guidance. For navigation purposes, kinematic velocity, geodetic height and more state information can be derived from air data, accounting for wind velocity vector and true atmosphere.
The underlying true physical process is of vast complexity and simple but efficient online dynamic models for wind and atmosphere are used together with online estimation techniques. The validity of the air data measurements require both limited angles of attack and sideslip and a minimum air pressure and hence velocity. Probes and vanes are mounted outside the aircraft and are vulnerable regarding icing or bird strike and must hence be provided redundant.
Air data are conventionally used in so-called Air Data Attitude/Heading Reference Systems (AD-AHRS).
Literature
- W. Gracey, Measurement of aircraft speed and altitude: NASA Reference Publication 1046. New York: Wiley, 1981.
- F. Trenkle and M. Reinhardt, AGARD Flight Test Instrumentation Series. Volume 2. In-Flight Temperature Measurements. Ft. Belvoir: Defense Technical Information Center, 1973.
- E. A. Haering, Airdata measurement and calibration. Edwards, Calif: National Aeronautics and Space Administration, Dryden Flight Research Center, 1995.
- W. Gracey, Summary of methods of measuring angle of attack on aircraft. Washington, DC: National Advisory Committee for Aeronautics, 1958.
- I. Moir, A. G. Seabridge, and M. Jukes, Civil avionic systems, 2nd ed. Chichester, West Sussex: Wiley, 2013.
- J. Roskam and C.-T. E. Lan, Airplane aerodynamics and performance. Lawrence, Kan.: Darkorporation, 1997.
Aerodynamic Navigation
Aerodynamic flight of a conventional, fixed-wing aircraft has been intensively studied and is a well-known physical process. The governing aerodynamic forces and moments can be described by reduced order models suitable for online evaluation in good precision.
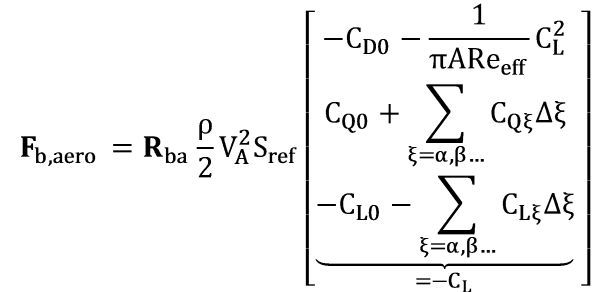
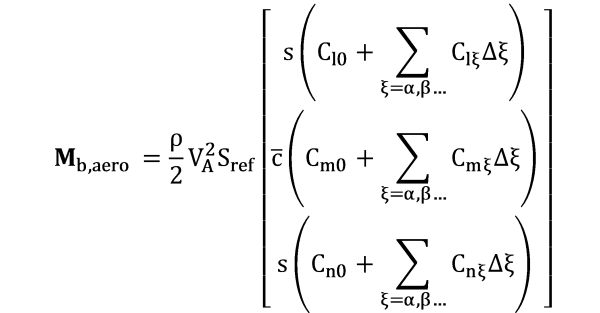
with the dimensionless coordinates of the linear aerodynamics model ![]() , reference wing area
, reference wing area ![]() , semi span
, semi span ![]() , mean aerodynamic chord
, mean aerodynamic chord ![]() and the Oswald efficiency factor
and the Oswald efficiency factor ![]() . The translational part of the aerodynamic ordinary differential equations once integrates the forces to linear velocity and twice to position. The rotational part of the aerodynamic ordinary differential equations one integrates moments to angular velocity and twice to angles. The translational and rotational aerodynamic model equations are coupled, hence the integrations are performed simultaneously. The flying platform under consideration is described by a set of aerodynamic coefficients. Thrust and control surface deflections describe the input to the aerodynamic model. The aerodynamic model can be used for navigational purposes if and only if the domain of definition of model and coefficients is not violated and a minimum velocity is given.
. The translational part of the aerodynamic ordinary differential equations once integrates the forces to linear velocity and twice to position. The rotational part of the aerodynamic ordinary differential equations one integrates moments to angular velocity and twice to angles. The translational and rotational aerodynamic model equations are coupled, hence the integrations are performed simultaneously. The flying platform under consideration is described by a set of aerodynamic coefficients. Thrust and control surface deflections describe the input to the aerodynamic model. The aerodynamic model can be used for navigational purposes if and only if the domain of definition of model and coefficients is not violated and a minimum velocity is given.
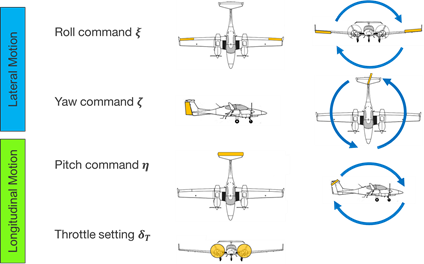
Literature
- B. L. Stevens and F. L. Lewis, Aircraft control and simulation, 2nd ed. Hoboken NJ: Wiley, 2003.
- J. D. Anderson, Fundamentals of aerodynamics, 5th ed. New York: McGraw-Hill, 2011.
- B. Etkin and L. D. Reid, Dynamics of flight: Stability and control, 3rd ed. New York: Wiley, 1996.
- J. Roskam and C.-T. E. Lan, Airplane aerodynamics and performance. Lawrence, Kan.: Darkorporation, 1997.
- R. F. Stengel, Flight dynamics. Princeton N.J.: Princeton University Press, 2004.
Surface-Ranging Navigation

In surface-ranging navigation an active range sensor is used as navigation aid. The ranging sensor is commonly body-fixed mounted and thus scans the Earth’s surface along the trajectory. Slant range measurements are inherent to the approach. Typically either an radar altimeter or a laser altimeter are used for this purpose. Radar altimeters provide comparably large measurement coils and thus are inherently more tolerant to slant range measurements. For applications with low dynamic platforms, like civil transport aircraft, the radar reflections may be even expected to stem from below the aircraft. For laser altimeters the reflecting spot on the surface is quite obvious due to its pencil beam, but slant range compensations then appear mandatory for almost all not straight and levelled flight situations.
When from the navigated trajectory the altimeter measured height above ground according to the current platform orientation is compensated, some surface track is derived which can be matched with a digital surface model (DSM) of sufficient resolution and accuracy. This approach assumes that platform velocity and orientation contribute just to second order to the error chain and thus the position error is the only error source of first order, i.e. the measured surface track is just dislocated from truth without deformation or orientation errors. The length of the measurement history or surface track for matching is taken such that on the one hand it is sufficiently long for the “wavelength” of the surface variation under consideration and on the other hand not long enough that drifts on velocity or orientation cause some sever deformation of the surface track.
Surface preference directions or even ambiguities cause that the “matching residual” does not provide the desired precision. The less rough and unique the surface along the surface track, the lower the altimeter measurement frequency, the larger the altimeter measurement error, the less precise the inertial navigation system or the biased the (barometric) altitude aiding are, the more nonlinear the problem becomes. Terrain linearization approaches have shown performance problems whenever the terrain within the current position uncertainty region cannot in sufficient accuracy be considered as planar. When a DSM is not available for matching it can be generated on-the-fly by an approach called simultaneous localization and mapping (SLAM).
Literature
- HOSTETLER, “Optimal terrain-aided navigation systems,” in Guidance, Navigation, and Control and Co-located Conferences, Guidance and Control Conference: American Institute of Aeronautics and Astronautics, 1978.
- Bergman, L. Ljung, and F. Gustafsson, “Terrain navigation using Bayesian statistics,” IEEE Control Syst. Mag, vol. 19, no. 3, pp. 33–40, 1999.
- Bar-Gill, P. Ben-Ezra, and I. Y. Bar-Itzhack, “Improvement of terrain-aided navigation via trajectory optimization,” IEEE Trans. Contr. Syst. Technol, vol. 2, no. 4, pp. 336–342, 1994.
- S. Anindya and E. A. Wan, “Dual Kalman filters for autonomous terrain aided navigation in unknown environments,” in 2005 IEEE International Joint Conference on Neural Networks, 2005
- Johnson, W. Tang, and G. Howell, “Terrain aided navigation using maximum a posteriori estimation,” in IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences, pp. 464–469.
- Paris and J.-P. Le Cadre, “Planning for terrain-aided navigation,” in Fifth International Conference on Information Fusion, pp. 1007–1014.
- Williams and I. Mahon, “A Terrain-Aided Tracking Algorithm for Marine Systems,” in Springer Tracts in Advanced Robotics, Field and Service Robotics, S. Yuta, H. Asama, E. Prassler, T. Tsubouchi, and S. Thrun, Eds.: Springer Berlin Heidelberg, 2006, pp. 93-102.
- Enns and D. Morrell, “Terrain-aided navigation using the Viterbi algorithm,” Journal of Guidance, Control, and Dynamics, vol. 18, no. 6, pp. 1444–1449, http://dx.doi.org/10.2514/3.21566, 1995.
- Montemerlo, S. Thrun, and B. Siciliano, FastSLAM: A scalable method for the simultaneous localization and mapping problem in robotics. Berlin: Springer, 2007.
- Laugier and R. Chatila, Autonomous navigation in dynamic environments. Berlin, New York: Springer, 2007.
| ⇦ Satellite Navigation | return to overview | Data Fusion ⇨ |